C Program For Arithmetic Coding For Data
I am trying to create an application that stores stock prices with high precision. Currently I am using a double to do so. To save up on memory can I use any other data type? I know this has something to do with fixed point arithmetic, but I can't figure it out.
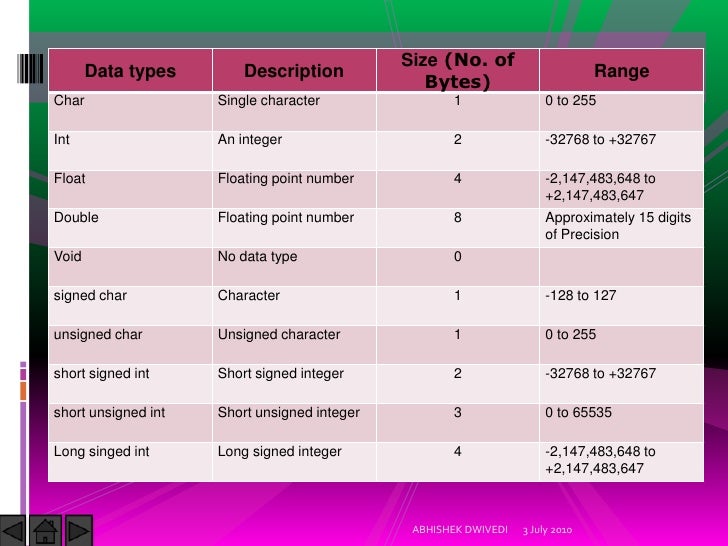
C compiler data types. Always match data type to data characteristics!. Variable type indicates how data i s represented. #bits determines range of numeric values. signed/unsigned determines which arithmetic/relational operators are to be used by the compiler. non-numeric data should be “unsigned”.
- This program takes an arithmetic operator (+, -,., /) and two operands from an user and performs the operation on those two operands depending upon the operator entered by user. C Program to Subtract Complex Number Using Operator Overloading. C Operator Overloading. Increment and Decrement - Operator Overloading in C Programming.
- Arithmetic coding is a data compression technique that encodes data (the data string) by creating a. One recursion of the algorithm handles one data symbol.
4 Answers
The idea behind fixed-point arithmetic is that you store the values multiplied by a certain amount, use the multiplied values for all calculus, and divide it by the same amount when you want the result. The purpose of this technique is to use integer arithmetic (int, long...) while being able to represent fractions.
The usual and most efficient way of doing this in C is by using the bits shifting operators (<< and >>). Shifting bits is a quite simple and fast operation for the ALU and doing this have the property to multiply (<<) and divide (>>) the integer value by 2 on each shift (besides, many shifts can be done for exactly the same price of a single one). Of course, the drawback is that the multiplier must be a power of 2 (which is usually not a problem by itself as we don't really care about that exact multiplier value).
Now let's say we want to use 32 bits integers for storing our values. We must choose a power of 2 multiplier. Let's divide the cake in two, so say 65536 (this is the most common case, but you can really use any power of 2 depending on your needs in precision). This is 216 and the 16 here means that we will use the 16 least significant bits (LSB) for the fractional part. The rest (32 - 16 = 16) is for the most significant bits (MSB), the integer part.
Let's put this in code:
This is the value you must put in store (structure, database, whatever). Note that int is not necessarily 32 bits in C even though it is mostly the case nowadays. Also without further declaration, it is signed by default. You can add unsigned to the declaration to be sure. Better than that, you can use uint32_t or uint_least32_t (declared in stdint.h) if your code highly depends on the integer bit size (you may introduce some hacks about it). In doubt, use a typedef for your fixed-point type and you're safer.
When you want to do calculus on this value, you can use the 4 basic operators: +, -, * and /. You have to keep in mind that when adding and subtracting a value (+ and -), that value must also be shifted. Let's say we want to add 10 to our 500 price:
But for multiplication and division (* and /), the multiplier/divisor must NOT be shifted. Let's say we want to multiply by 3:
Now let's make things more interesting by dividing the price by 4 so we make up for a non-zero fractional part:
That's all about the rules. When you want to retrieve the real price at any point, you must right-shift:
If you need the fractional part, you must mask it out:
Of course, this value is not what we can call a decimal fraction, in fact it is an integer in the range [0 - 65535]. But it maps exactly with the decimal fraction range [0 - 0.9999...]. In other words, mapping looks like: 0 => 0, 32768 => 0.5, 65535 => 0.9999...
An easy way to see it as a decimal fraction is to resort to C built-in float arithmetic at this point:
But if you don't have FPU support (either hardware or software), you can use your new skills like this for complete price:
The number of 0's in the expression is roughly the number of digits you want after the decimal point. Don't overestimate the number of 0's given your fraction precision (no real trap here, that's quite obvious). Don't use simple long as sizeof(long) can be equal to sizeof(int). Use long long in case int is 32 bits as long long is guaranted to be 64 bits minimum (or use int64_t, int_least64_t and such, declared in stdint.h). In other words, use a type twice the size of your fixed-point type, that's fair enough. Finally, if you don't have access to >= 64 bits types, maybe it's time to exercice emulating them, at least for your output.
These are the basic ideas behind fixed-point arithmetics.
Be careful with negative values. It can becomes tricky sometimes, especially when it's time to show the final value. Besides, C is implementation-defined about signed integers (even though platforms where this is a problem are very uncommon nowadays). You should always make minimal tests in your environment to make sure everything goes as expected. If not, you can hack around it if you know what you do (I won't develop on this, but this has something to do with arithmetic shift vs logical shift and 2's complement representation). With unsigned integers however, you're mostly safe whatever you do as behaviors are well defined anyway.
Also take note that if a 32 bits integer can not represent values bigger than 232 - 1, using fixed-point arithmetic with 216 limits your range to 216 - 1! (and divide all of this by 2 with signed integers, which in our example would leave us with an available range of 215 - 1). The goal is then to choose a SHIFT_AMOUNT suitable to the situation. This is a tradeoff between integer part magnitude and fractional part precision.
Now for the real warnings: this technique is definitely not suitable in areas where precision is a top priority (financial, science, military...). Usual floating point (float/double) are also often not precise enough, even though they have better properties than fixed-point overall. Fixed-point has the same precision whatever the value (this can be an advantage in some cases), where floats precision is inversely proportional to the value magnitude (ie. the lower the magnitude, the more precision you get... well, this is more complex than that but you get the point). Also floats have a much greater magnitude than the equivalent (in number of bits) integers (fixed-point or not), to the cost of a loss of precision with high values (you can even reach a point of magnitude where adding 1 or even greater values will have no effect at all, something that cannot happen with integers).
If you work in those sensible areas, you're better off using libraries dedicated to the purpose of arbitrary precision (go take a look at gmplib, it's free). In computing science, essentially, gaining precision is about the number of bits you use to store your values. You want high precision? Use bits. That's all.
I see two options for you. If you are working in the financial services industry, there are probably standards that your code should comply with for precision and accuracy, so you'll just have to go along with that, regardless of memory cost. I understand that that business is generally well funded, so paying for more memory shouldn't be a problem. :)
If this is for personal use, then for maximum precision I recommend you use integers and multiply all prices by a fixed factor before storage. For example, if you want things accurate to the penny (probably not good enough), multiply all prices by 100 so that your unit is effectively cents instead of dollars and go from there. If you want more precision, multiply by more. For example, to be accurate to the hundredth of a cent (a standard that I have heard is commonly applied), multiply prices by 10000 (100 * 100).
Now with 32-bit integers, multiplying by 10000 leaves little room for large numbers of dollars. A practical 32-bit limit of 2 billion means that only prices as high as $20000 can be expressed: 2000000000 / 10000 = 20000. This gets worse if you multiply that 20000 by something, as there may be no room to hold the result. For this reason, I recommend using 64-bit integers (long long). Even if you multiply all prices by 10000, there is still plenty of headroom to hold large values, even across multiplications.
The trick with fixed-point is that whenever you do a calculation you need to remember that each value is really an underlying value multiplied by a constant. Before you add or subtract, you need to multiply values with a smaller constant to match those with a bigger constant. After you multiply, you need to divide by something to get the result back to being multiplied by the desired constant. If you use a non-power of two as your constant, you'll have to do an integer divide, which is expensive, time-wise. Many people use powers of two as their constants, so they can shift instead of divide.
If all this seems complicated, it is. I think the easiest option is to use doubles and buy more RAM if you need it. They have 53 bits of precision, which is roughly 9 quadrillion, or almost 16 decimal digits. Yes, you still might lose pennies when you are working with billions, but if you care about that, you're not being a billionaire the right way. :)
Randall CookRandall Cook@Alex gave a fantastic answer here. However, I wanted to add some improvements to what he's done, by, for example, demonstrating how to do emulated-float (using integers to act like floats) rounding to any desired decimal place. I demonstrate that in my code below. I went a lot farther, though, and ended up writing a whole code tutorial to teach myself fixed-point math. Here it is:
fixed_point_math tutorial
- A tutorial-like practice code to learn how to do fixed-point math, manual 'float'-like prints using integers only, 'float'-like integer rounding, and fractional fixed-point math on large integers.
If you really want to learn fixed-point math, I think this is valuable code to carefully go through, but it took me an entire weekend to write, so expect it to take you perhaps a couple hours to thoroughly go through it all. The basics of the rounding stuff can be found right at the top section, however, and learned in just a few minutes.
Full code on GitHub: https://github.com/ElectricRCAircraftGuy/fixed_point_math.
Or, below (truncated, because Stack Overflow won't allow that many characters):
Output:
gabriel$ cp fixed_point_math.cpp fixed_point_math_copy.c && gcc -Wall -std=c99 -o ./bin/fixed_point_math_c > fixed_point_math_copy.c && ./bin/fixed_point_math_c
Begin.
fraction bits = 16.
whole number bits = 16.
max whole number = 65535.
price as a true double is 219.857142857.
price as integer is 219.
price fractional part is 56173 (of 65536).
price fractional part as decimal is 0.857132 (56173/65536).
price (manual float, 0 digits after decimal) is 219.
price (manual float, 1 digit after decimal) is 219.8.
price (manual float, 2 digits after decimal) is 219.85.
price (manual float, 3 digits after decimal) is 219.857.
price (manual float, 4 digits after decimal) is 219.8571.
price (manual float, 5 digits after decimal) is 219.85713. < Fixed-point math decimal error first
starts to get introduced here since the fixed point resolution (1/65536) now has lower resolution
than the base-10 resolution (which is 1/100000) at this decimal place. Decimal error may not show
up at this decimal location, per say, but definitely will for all decimal places hereafter.
price (manual float, 6 digits after decimal) is 219.857131.
WITH MANUAL INTEGER-BASED ROUNDING:
addend0 = 32768.
addend1 = 3276.
addend2 = 327.
addend3 = 32.
addend4 = 3.
addend5 = 0.
rounded price (manual float, rounded to 0 digits after decimal) is 220.
rounded price (manual float, rounded to 1 digit after decimal) is 219.9.
rounded price (manual float, rounded to 2 digits after decimal) is 219.86.
rounded price (manual float, rounded to 3 digits after decimal) is 219.857.
rounded price (manual float, rounded to 4 digits after decimal) is 219.8571.
rounded price (manual float, rounded to 5 digits after decimal) is 219.85713.
RELATED CONCEPT: DOING LARGE-INTEGER MATH WITH SMALL INTEGER TYPES:
EXAMPLE 1
65401 * 16/127 = 8239. < true answer
1st approach (divide then multiply):
num16_result = 8224. < Loses bits that right-shift out during the initial divide.
2nd approach (split into 2 8-bit sub-numbers with bits at far right):
num16_result = 8207. < Loses bits that right-shift out during the divide.
3rd approach (split into 2 8-bit sub-numbers with bits centered):
num16_result = 8239. < Perfect! Retains the bits that right-shift during the divide.
EXAMPLE 2
65401 * 99/127 = 50981. < true answer
1st approach (divide then multiply):
num16_result = 50886. < Loses bits that right-shift out during the initial divide.
2nd approach (split into 2 8-bit sub-numbers with bits at far right):
num16_result = 50782. < Loses bits that right-shift out during the divide.
3rd approach (split into 2 8-bit sub-numbers with bits centered):
num16_result = 1373. < Completely wrong due to overflow during the multiply.
4th approach (split into 4 4-bit sub-numbers with bits centered):
num16_result = 15870. < Completely wrong due to overflow during the multiply.
5th approach (split into 8 2-bit sub-numbers with bits centered):
num16_result = 50922. < Loses a few bits that right-shift out during the divide.
6th approach (split into 16 1-bit sub-numbers with bits skewed left):
num16_result = 50963. < Loses the fewest possible bits that right-shift out during the divide.
7th approach (split into 16 1-bit sub-numbers with bits skewed left):
num16_result = 50963. < [same as 6th approach] Loses the fewest possible bits that right-shift out during the divide.
[BEST APPROACH OF ALL] 8th approach (split into 16 1-bit sub-numbers with bits skewed left, w/integer rounding during division):
num16_result = 50967. < Loses the fewest possible bits that right-shift out during the divide,
& has better accuracy due to rounding during the divide.
References:
- https://github.com/ElectricRCAircraftGuy/eRCaGuy_analogReadXXbit/blob/master/eRCaGuy_analogReadXXbit.cpp - see 'Integer math rounding notes' at bottom.
I would not recommend you to do so, if your only purpose is to save memory. The error in the calculation of price can be accumulated and you are going to screw up on it.
If you really want to implement similar stuff, can you just take the minimum interval of the price and then directly use int and integer operation to manipulate your number? You only need to convert it to the floating point number when display, which make your life easier.
Not the answer you're looking for? Browse other questions tagged cfixed-point or ask your own question.
I am trying to create an application that stores stock prices with high precision. Currently I am using a double to do so. To save up on memory can I use any other data type? I know this has something to do with fixed point arithmetic, but I can't figure it out.
Jonathan Leffler
4 Answers
The idea behind fixed-point arithmetic is that you store the values multiplied by a certain amount, use the multiplied values for all calculus, and divide it by the same amount when you want the result. The purpose of this technique is to use integer arithmetic (int, long...) while being able to represent fractions.
The usual and most efficient way of doing this in C is by using the bits shifting operators (<< and >>). Shifting bits is a quite simple and fast operation for the ALU and doing this have the property to multiply (<<) and divide (>>) the integer value by 2 on each shift (besides, many shifts can be done for exactly the same price of a single one). Of course, the drawback is that the multiplier must be a power of 2 (which is usually not a problem by itself as we don't really care about that exact multiplier value).
Now let's say we want to use 32 bits integers for storing our values. We must choose a power of 2 multiplier. Let's divide the cake in two, so say 65536 (this is the most common case, but you can really use any power of 2 depending on your needs in precision). This is 216 and the 16 here means that we will use the 16 least significant bits (LSB) for the fractional part. The rest (32 - 16 = 16) is for the most significant bits (MSB), the integer part.
Let's put this in code:
This is the value you must put in store (structure, database, whatever). Note that int is not necessarily 32 bits in C even though it is mostly the case nowadays. Also without further declaration, it is signed by default. You can add unsigned to the declaration to be sure. Better than that, you can use uint32_t or uint_least32_t (declared in stdint.h) if your code highly depends on the integer bit size (you may introduce some hacks about it). In doubt, use a typedef for your fixed-point type and you're safer.
When you want to do calculus on this value, you can use the 4 basic operators: +, -, * and /. You have to keep in mind that when adding and subtracting a value (+ and -), that value must also be shifted. Let's say we want to add 10 to our 500 price:
But for multiplication and division (* and /), the multiplier/divisor must NOT be shifted. Let's say we want to multiply by 3:
Now let's make things more interesting by dividing the price by 4 so we make up for a non-zero fractional part:
That's all about the rules. When you want to retrieve the real price at any point, you must right-shift:
If you need the fractional part, you must mask it out:
Of course, this value is not what we can call a decimal fraction, in fact it is an integer in the range [0 - 65535]. But it maps exactly with the decimal fraction range [0 - 0.9999...]. In other words, mapping looks like: 0 => 0, 32768 => 0.5, 65535 => 0.9999...
An easy way to see it as a decimal fraction is to resort to C built-in float arithmetic at this point:
But if you don't have FPU support (either hardware or software), you can use your new skills like this for complete price:
The number of 0's in the expression is roughly the number of digits you want after the decimal point. Don't overestimate the number of 0's given your fraction precision (no real trap here, that's quite obvious). Don't use simple long as sizeof(long) can be equal to sizeof(int). Use long long in case int is 32 bits as long long is guaranted to be 64 bits minimum (or use int64_t, int_least64_t and such, declared in stdint.h). In other words, use a type twice the size of your fixed-point type, that's fair enough. Finally, if you don't have access to >= 64 bits types, maybe it's time to exercice emulating them, at least for your output.
These are the basic ideas behind fixed-point arithmetics.
Be careful with negative values. It can becomes tricky sometimes, especially when it's time to show the final value. Besides, C is implementation-defined about signed integers (even though platforms where this is a problem are very uncommon nowadays). You should always make minimal tests in your environment to make sure everything goes as expected. If not, you can hack around it if you know what you do (I won't develop on this, but this has something to do with arithmetic shift vs logical shift and 2's complement representation). With unsigned integers however, you're mostly safe whatever you do as behaviors are well defined anyway.
Also take note that if a 32 bits integer can not represent values bigger than 232 - 1, using fixed-point arithmetic with 216 limits your range to 216 - 1! (and divide all of this by 2 with signed integers, which in our example would leave us with an available range of 215 - 1). The goal is then to choose a SHIFT_AMOUNT suitable to the situation. This is a tradeoff between integer part magnitude and fractional part precision.
Now for the real warnings: this technique is definitely not suitable in areas where precision is a top priority (financial, science, military...). Usual floating point (float/double) are also often not precise enough, even though they have better properties than fixed-point overall. Fixed-point has the same precision whatever the value (this can be an advantage in some cases), where floats precision is inversely proportional to the value magnitude (ie. the lower the magnitude, the more precision you get... well, this is more complex than that but you get the point). Also floats have a much greater magnitude than the equivalent (in number of bits) integers (fixed-point or not), to the cost of a loss of precision with high values (you can even reach a point of magnitude where adding 1 or even greater values will have no effect at all, something that cannot happen with integers).
If you work in those sensible areas, you're better off using libraries dedicated to the purpose of arbitrary precision (go take a look at gmplib, it's free). In computing science, essentially, gaining precision is about the number of bits you use to store your values. You want high precision? Use bits. That's all.
I see two options for you. If you are working in the financial services industry, there are probably standards that your code should comply with for precision and accuracy, so you'll just have to go along with that, regardless of memory cost. I understand that that business is generally well funded, so paying for more memory shouldn't be a problem. :)
C Program For Arithmetic Coding In Data Compression
If this is for personal use, then for maximum precision I recommend you use integers and multiply all prices by a fixed factor before storage. For example, if you want things accurate to the penny (probably not good enough), multiply all prices by 100 so that your unit is effectively cents instead of dollars and go from there. If you want more precision, multiply by more. For example, to be accurate to the hundredth of a cent (a standard that I have heard is commonly applied), multiply prices by 10000 (100 * 100).
Binary Code In Data Compression
Now with 32-bit integers, multiplying by 10000 leaves little room for large numbers of dollars. A practical 32-bit limit of 2 billion means that only prices as high as $20000 can be expressed: 2000000000 / 10000 = 20000. This gets worse if you multiply that 20000 by something, as there may be no room to hold the result. For this reason, I recommend using 64-bit integers (long long). Even if you multiply all prices by 10000, there is still plenty of headroom to hold large values, even across multiplications.
The trick with fixed-point is that whenever you do a calculation you need to remember that each value is really an underlying value multiplied by a constant. Before you add or subtract, you need to multiply values with a smaller constant to match those with a bigger constant. After you multiply, you need to divide by something to get the result back to being multiplied by the desired constant. If you use a non-power of two as your constant, you'll have to do an integer divide, which is expensive, time-wise. Many people use powers of two as their constants, so they can shift instead of divide.
If all this seems complicated, it is. I think the easiest option is to use doubles and buy more RAM if you need it. They have 53 bits of precision, which is roughly 9 quadrillion, or almost 16 decimal digits. Yes, you still might lose pennies when you are working with billions, but if you care about that, you're not being a billionaire the right way. :)
Randall CookRandall Cook@Alex gave a fantastic answer here. However, I wanted to add some improvements to what he's done, by, for example, demonstrating how to do emulated-float (using integers to act like floats) rounding to any desired decimal place. I demonstrate that in my code below. I went a lot farther, though, and ended up writing a whole code tutorial to teach myself fixed-point math. Here it is:
fixed_point_math tutorial
- A tutorial-like practice code to learn how to do fixed-point math, manual 'float'-like prints using integers only, 'float'-like integer rounding, and fractional fixed-point math on large integers.
If you really want to learn fixed-point math, I think this is valuable code to carefully go through, but it took me an entire weekend to write, so expect it to take you perhaps a couple hours to thoroughly go through it all. The basics of the rounding stuff can be found right at the top section, however, and learned in just a few minutes.
Full code on GitHub: https://github.com/ElectricRCAircraftGuy/fixed_point_math.
Or, below (truncated, because Stack Overflow won't allow that many characters):
Output:
gabriel$ cp fixed_point_math.cpp fixed_point_math_copy.c && gcc -Wall -std=c99 -o ./bin/fixed_point_math_c > fixed_point_math_copy.c && ./bin/fixed_point_math_c
Begin.
fraction bits = 16.
whole number bits = 16.
max whole number = 65535.
price as a true double is 219.857142857.
price as integer is 219.
price fractional part is 56173 (of 65536).
price fractional part as decimal is 0.857132 (56173/65536).
price (manual float, 0 digits after decimal) is 219.
price (manual float, 1 digit after decimal) is 219.8.
price (manual float, 2 digits after decimal) is 219.85.
price (manual float, 3 digits after decimal) is 219.857.
price (manual float, 4 digits after decimal) is 219.8571.
price (manual float, 5 digits after decimal) is 219.85713. < Fixed-point math decimal error first
starts to get introduced here since the fixed point resolution (1/65536) now has lower resolution
than the base-10 resolution (which is 1/100000) at this decimal place. Decimal error may not show
up at this decimal location, per say, but definitely will for all decimal places hereafter.
price (manual float, 6 digits after decimal) is 219.857131.
WITH MANUAL INTEGER-BASED ROUNDING:
addend0 = 32768.
addend1 = 3276.
addend2 = 327.
addend3 = 32.
addend4 = 3.
addend5 = 0.
rounded price (manual float, rounded to 0 digits after decimal) is 220.
rounded price (manual float, rounded to 1 digit after decimal) is 219.9.
rounded price (manual float, rounded to 2 digits after decimal) is 219.86.
rounded price (manual float, rounded to 3 digits after decimal) is 219.857.
rounded price (manual float, rounded to 4 digits after decimal) is 219.8571.
rounded price (manual float, rounded to 5 digits after decimal) is 219.85713.
RELATED CONCEPT: DOING LARGE-INTEGER MATH WITH SMALL INTEGER TYPES:
EXAMPLE 1
65401 * 16/127 = 8239. < true answer
1st approach (divide then multiply):
num16_result = 8224. < Loses bits that right-shift out during the initial divide.
2nd approach (split into 2 8-bit sub-numbers with bits at far right):
num16_result = 8207. < Loses bits that right-shift out during the divide.
3rd approach (split into 2 8-bit sub-numbers with bits centered):
num16_result = 8239. < Perfect! Retains the bits that right-shift during the divide.
EXAMPLE 2
65401 * 99/127 = 50981. < true answer
1st approach (divide then multiply):
num16_result = 50886. < Loses bits that right-shift out during the initial divide.
2nd approach (split into 2 8-bit sub-numbers with bits at far right):
num16_result = 50782. < Loses bits that right-shift out during the divide.
3rd approach (split into 2 8-bit sub-numbers with bits centered):
num16_result = 1373. < Completely wrong due to overflow during the multiply.
4th approach (split into 4 4-bit sub-numbers with bits centered):
num16_result = 15870. < Completely wrong due to overflow during the multiply.
5th approach (split into 8 2-bit sub-numbers with bits centered):
num16_result = 50922. < Loses a few bits that right-shift out during the divide.
6th approach (split into 16 1-bit sub-numbers with bits skewed left):
num16_result = 50963. < Loses the fewest possible bits that right-shift out during the divide.
7th approach (split into 16 1-bit sub-numbers with bits skewed left):
num16_result = 50963. < [same as 6th approach] Loses the fewest possible bits that right-shift out during the divide.
[BEST APPROACH OF ALL] 8th approach (split into 16 1-bit sub-numbers with bits skewed left, w/integer rounding during division):
num16_result = 50967. < Loses the fewest possible bits that right-shift out during the divide,
& has better accuracy due to rounding during the divide.
References:
- https://github.com/ElectricRCAircraftGuy/eRCaGuy_analogReadXXbit/blob/master/eRCaGuy_analogReadXXbit.cpp - see 'Integer math rounding notes' at bottom.
I would not recommend you to do so, if your only purpose is to save memory. The error in the calculation of price can be accumulated and you are going to screw up on it.
If you really want to implement similar stuff, can you just take the minimum interval of the price and then directly use int and integer operation to manipulate your number? You only need to convert it to the floating point number when display, which make your life easier.